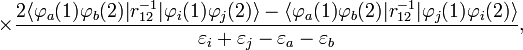Teoria perturbativa di Møller-Plesset

La teoria perturbativa di Møller-Plesset (MPn) è un metodo ab initio post-Hartree-Fock utilizzato nel calcolo computazionale di chimica quantistica. Rappresenta un perfezionamento del metodo Hartree-Fock ottenuto tenendo conto della correlazione elettronica sfruttando la teoria perturbativa, solitamente del secondo (MP2), terzo (MP3) o quarto ordine (MP4).

La teoria perturbativa rappresenta una trattazione quantomeccanica che esprime matematicamente l'effetto generato da una perturbazione esterna sul sistema oggetto di studio, nel caso chimico quantistico ciò è particolarmente utile considerando che in una reazione chimica spesso si trovano a interagire dipoli molecolari o specie ioniche alle quali è associato un certo valore di campo elettrico. Il classico operatore hamiltoniano non perturbato ${\displaystyle {\hat {H}}_{0}}$ assume una forma estesa addizionandogli un fattore perturbativo ${\displaystyle {\hat {V}}}$:

${\displaystyle {\hat {H}}={\hat {H}}_{0} \lambda {\hat {V}}}$,

dove λ è un parametro che descrive l'entità della perturbazione. La funzione d'onda di Hartree-Fock è un'autofunzione approssimata dell'hamiltoniano corretto ma diviene un'autofunzione esatta considerando la somma dei singoli operatori di Fock ${\displaystyle {\hat {H}}_{0}}$. La perturbazione rappresenta matematicamente la differenza tra l'hamiltoniano effettivo e l'hamiltoniano di Hartree-Fock originario (sistema non perturbato), cioè un contributo energetico dovuto all'interazione delle cariche elettriche che l'Hartree-Fock classico considera solamente come effetto medio (questo è uno degli assunti fondamentali del metodo Hartree-Fock). Se l'entità della perturbazione è sufficientemente piccola, la risultante funzione d'onda ed energia può essere espressa in serie di potenze in λ:

${\displaystyle \Psi =\lim _{n\to \infty }\sum _{i}^{n}\lambda ^{i}\Psi ^{(i)}}$,

${\displaystyle E=\lim _{n\to \infty }\sum _{i}^{n}\lambda ^{i}E^{(i)}}$.

Introducendo queste serie di potenze nell'equazione di Schrödinger tempo-indipendente si ottiene

${\displaystyle \left({\hat {H}}_{0} \lambda V\right)\left(\sum _{i}^{n}\lambda ^{i}\Psi ^{(i)}\right)=\left(\sum _{i}^{n}\lambda ^{i}E^{(i)}\right)\left(\sum _{i}^{n}\lambda ^{i}\Psi ^{(i)}\right)}$.

Il coefficiente λ_i relativo all'orbitale ${\displaystyle \Psi _{i}}$ è genericamente espresso come

${\displaystyle \lambda _{i}={\frac {-\int \Psi _{i}^{*}{\hat {H}}\Psi _{0}d\tau }{E_{i}-E_{0}}}}$ .

La soluzione dell'equazione di Schrödinger per l'ordine 0 fornisce un valore di energia che rappresenta la somma delle energie degli orbitali elettronici. Nel caso dell'ordine 1 si ottiene una energia corretta di Hartree-Fock e la funzione d'onda. Per ottenere risultati diversi dal metodo Hartree-Fock è necessario superare il primo ordine. Il secondo (MP2),) il terzo (MP3) e il quarto ordine (MP4) sono i livelli standard applicati per la teoria di Møller-Plesset per il calcolo relativo a sistemi piccoli. Calcoli di ordini superiori sono possibili, ma vengono di rado utilizzati in pratica.

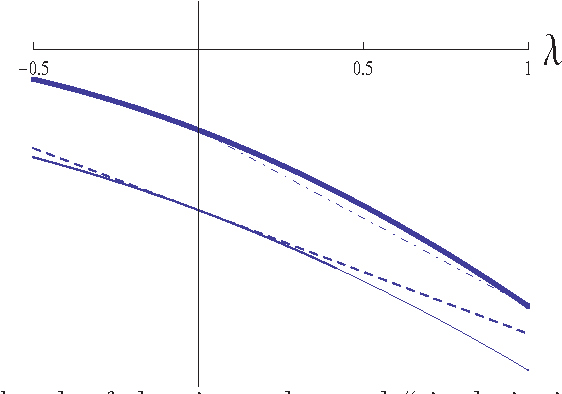
Studi sistematici sulla teoria MPn hanno dimostrato che il metodo non è necessariamente convergente a ordini superiori. Il tipo di convergenza tende ad essere variabile in relazione alla complessità del sistema studiato e all'insieme di funzioni d'onda di base utilizzate.

La teoria NEVPT è una applicazione della teoria di Møller-Plesset di secondo ordine per funzioni d'onda utilizzate nel metodo complete active space.

Note

Bibliografia

• Christian Møller e Milton S. Plesset, Note on an Approximation Treatment for Many-Electron Systems (abstract), in Phys. Rev., vol. 46, n. 7, 1934, pp. 618-622, DOI:10.1103/PhysRev.46.618.